
Now, we have the circle equation in standard form. This allows us to factor as another perfect square trinomial: Note that we grouped the +9 on the left with the x terms. So, we add 9 to both sides of the equation to get: Here, the x-coefficient is 6, so half of that gives us a result of 3. Remember that to complete the square, we take half of the x coefficient and square the result, then add it to both sides. Now we just need to complete the square for the expression with the x variable, x 2 + 6x. It is easy to see that the expression with the y variable, y 2 + 10y + 25, factors as a perfect square trinomial, (y + 5) 2: This circle is not in standard form, so we know we will need to complete the square for at least one variable.Īfter rearranging the terms so the variables are grouped together, we get: Example 2: Center Of A Circle From An Equation By Completing The Square For One Variable So, the center of the circle is (a, b) = (2, -4). Let’s say we want to find the center of the circle given by the equationĬomparing this to the standard form above, we can see that a = 2 and b = -4 (watch out for those negative signs: y – (-4) is the same as y + 4). Example 1: Center Of A Circle From An Equation In Standard Form If we are given an equation that is not in standard form, we will need to complete the square for one or both variables (x and y) first.
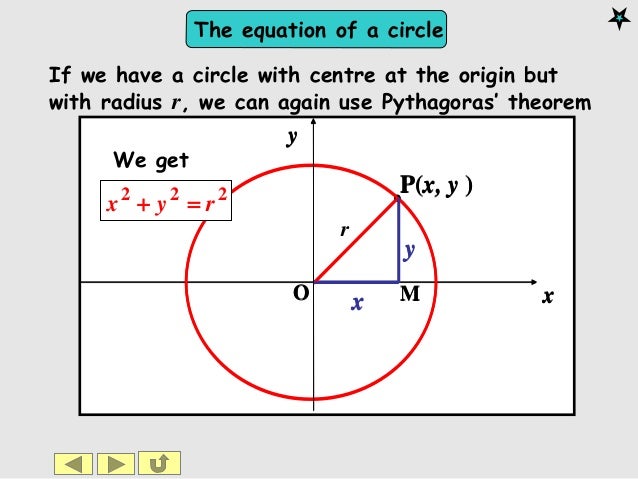

Where (a, b) is the center of the circle and r is the radius of the circle.

Remember that the equation of a circle in standard form is given by: Types of Circle Hooks - Which Type of Circle Hook Should You Be Using


 0 kommentar(er)
0 kommentar(er)
